2015 bacblanc.pdf

REMPLACEMENT 2015
Métropole - Réunion - Mayotte

BACCALAURÉAT PROFESSIONNEL
E4 CULTURE SCIENTIFIQUE ET TECHNOLOGIQUE : MATHÉMATIQUES
Toutes options

Durée : 2 heures
_____________________________________________________________________________________

Matériel(s) et document(s) autorisé(s) : Calculatrice
_____________________________________________________________________________________
Le sujet comporte 5 pages

_____________________________________________________________________________________
Les annexes A et B sont à rendre avec la copie
_____________________________________________________________________________________________

SUJET
EXERCICE 1 (4 points)
On a relevé dans une commune A, le montant du loyer, exprimé en euros, auprès de 200 familles.
Le tableau ci-dessous donne la répartition des familles selon ce montant.

Montant
du loyer

[300 ; 400[

[400 ; 500[

[500 ; 600[

[600 ; 700[

[700 ; 800[

[800 ; 900[

[900 ; 1000[

[1000 ; 1100[

12

26

62

40

32

17

8

3

en euros
Effectifs

1) En ramenant le montant du loyer au centre de chaque classe, déterminer la moyenne x et l’écart
type  de cette série statistique. On ne demande pas le détail des calculs qui pourront être conduits
à la calculatrice. Les résultats seront arrondis à 10 2 près.
2) La même étude a été menée dans une commune B. Les résultats obtenus sont les suivants :

x  632

  48,25
Déterminer la commune dans laquelle les montants des loyers sont les plus homogènes. Justifier la
réponse.

2015-PRO12-RPL-ME-RE-MA

1/5

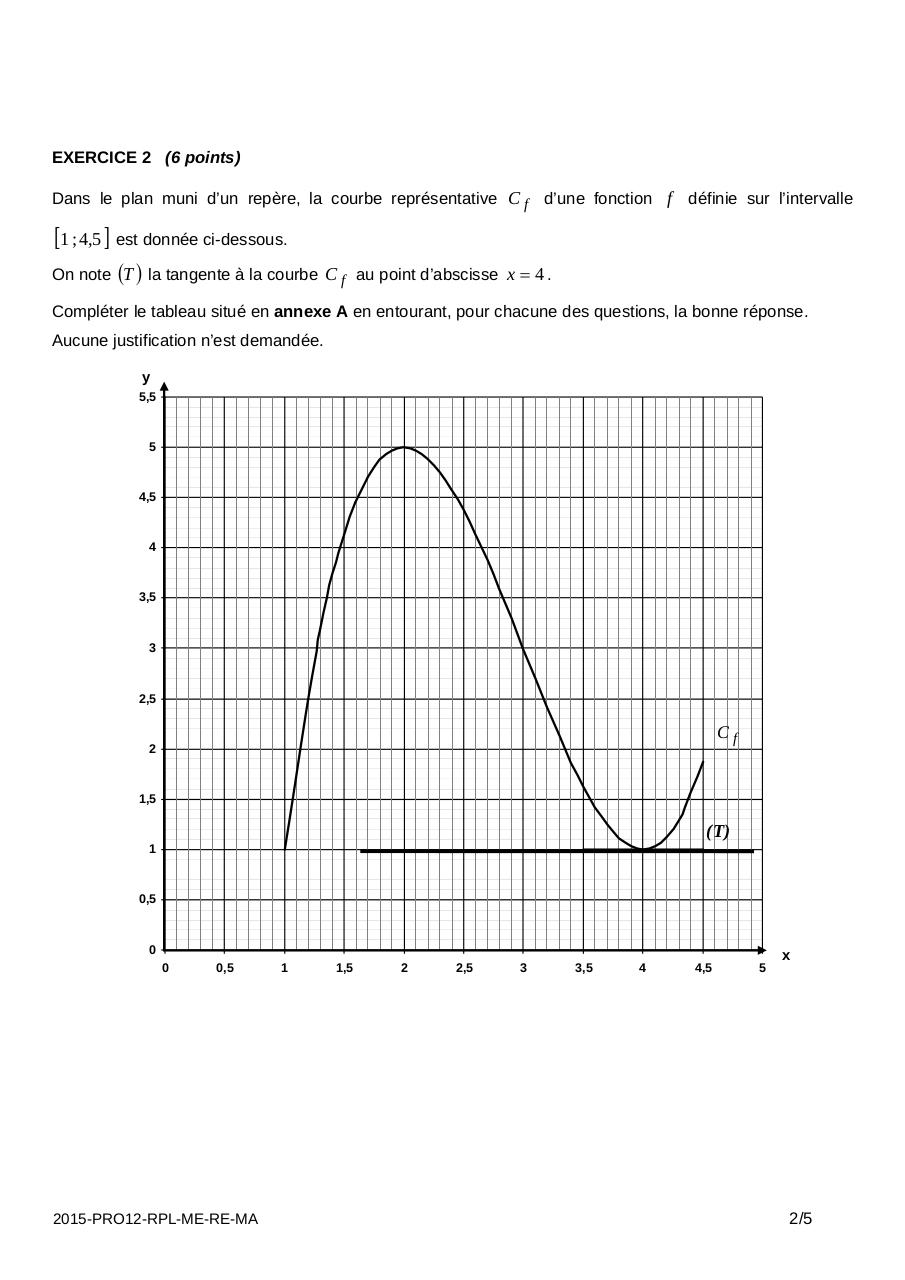
EXERCICE 2 (6 points)
Dans le plan muni d’un repère, la courbe représentative C f d’une fonction f définie sur l’intervalle

1 ; 4,5  est donnée ci-dessous.
On note T  la tangente à la courbe C f

au point d’abscisse x  4 .

Compléter le tableau situé en annexe A en entourant, pour chacune des questions, la bonne réponse.
Aucune justification n’est demandée.
y
5,5

5

4,5

4

3,5

3

2,5

Cf

2

1,5

(T)
1

0,5

0
0

0,5

2015-PRO12-RPL-ME-RE-MA

1

1,5

2

2,5

3

3,5

4

4,5

5

x

2/5

EXERCICE 3 (10 points)
Pour contrôler la pollution en milieu urbain, on étudie la concentration dans l’air de particules « fines ».
Suite à une étude menée à proximité d’une ville, on modélise la concentration de particules « fines » en un
lieu, en fonction de la distance qui le sépare du centre ville, par la fonction f définie sur l’intervalle  0 ; 13 
par :

f ( x) 18 e  0,4 x

f (x) représente la concentration, exprimée en g / m 3 , de particules « fines » en un lieu et x la distance,
exprimée en kilomètres, entre ce lieu et le centre ville.

1) Déterminer la concentration de particules « fines » présentes dans l’air à 4 kilomètres du centre ville.
Arrondir le résultat à 10 1 près.
2) Déterminer la concentration de particules « fines » présentes dans l’air au centre ville.
3) Soit f ' la fonction dérivée de la fonction f sur l’intervalle  0 ; 13  . Déterminer f ' ( x) .
4) Montrer que pour tout nombre x appartenant à l’intervalle  0 ; 13  , f ' ( x) est négatif.
5) En déduire le sens de variation de la fonction f sur l’intervalle  0 ; 13  .
6) Compléter le tableau de valeurs donné en annexe A. Arrondir les résultats à 10 1 près.
7) Construire, en annexe B, la courbe représentative de la fonction f sur l’intervalle  0 ; 13  dans le
plan muni d’un repère.
8) a) Résoudre l’équation f ( x)  3 . Arrondir le résultat à 10 1 près.
La méthode est laissée à l’appréciation du candidat (graphique, algébrique, à l’aide de la
calculatrice…).
b) Interpréter le résultat précédent dans le contexte de l’exercice.

Rappels :

Dérivées

f(x)

f’(x)

e ax

ae ax

a est un nombre réel.

2015-PRO12-RPL-ME-RE-MA

3/5

MINISTERE DE L’AGRICULTURE
EXAMEN :
Nom :
(EN MAJUSCULES)
Prénoms :

N° ne rien inscrire

Spécialité ou Option :
EPREUVE :

Date de naissance :

19

Centre d’épreuve :
Date :

ANNEXE A (à compléter et à rendre avec la copie)

N° ne rien inscrire

EXERCICE 2
Questions

Réponses proposées

1) L’image de 4 est :
2) L’équation f ( x)  1,5 admet
3) f ( x)  4,1 pour x appartenant à l’intervalle
4) f ' (4) est égal à
5) L’équation de la tangente (T ) est
6) I 

3

2 f ( x)dx

1

0

1,5

1 solution

Pas de
solution

3 solutions

1 ; 1,4

1,5 ; 2,6

 2,7 ; 4,5

1

0

2,6

x0

y 1

y  x4

3 I 5

6  I  10

12  I  20

EXERCICE 3

x

0

1

2

3

4

5

6

7

8

9

10

13

f(x)

2015-PRO12-RPL-ME-RE-MA

4/5

MINISTERE DE L’AGRICULTURE
EXAMEN :
Nom :
(EN MAJUSCULES)
Prénoms :

N° ne rien inscrire

Spécialité ou Option :
EPREUVE :

Date de naissance :

19

Centre d’épreuve :
Date :

ANNEXE B (à compléter et à rendre avec la copie)

N° ne rien inscrire

EXERCICE 3

y

19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0

0

1

2

3

2015-PRO12-NOR-ME-RE-MA

4

5

6

7

8

9

10

11

12

13

14

15

16

x

5/5